Next: 4 計算練習: の Fourier 係数 Up: 1 Mathematica で Fourier級数 Previous: 2 部分和のグラフを描く
Fourier級数の部分和が元の関数に近いことを確かめるには、 両方のグラフを描いて比較するのが良い。
上の例では、周期 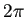 の周期関数を、
の周期関数を、
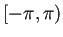 での値を指定することで定義した。
Mathematica でそれに相当することをするには、次のようにすればよい。
での値を指定することで定義した。
Mathematica でそれに相当することをするには、次のようにすればよい。
f0[x_]:=Abs[x] f[x_]:=f0[Mod[x,2Pi,-Pi]] g0[x_]:=Which[-Pi<x<0,-1,x==0||x==Pi,0,0<x<Pi,1] g[x_]:=g0[Mod[x,2Pi,-Pi]] |
Mod[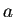 ,
, 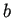 ,
, 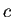 ] は、手短に言うと、
] は、手短に言うと、
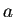 を
を 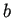 で割った余りを
で割った余りを 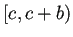 の範囲で求めてくれる。
つまり、
の範囲で求めてくれる。
つまり、
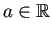 ,
, 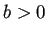 ,
,
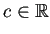 とするとき、
とするとき、
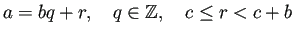
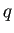 ,
, 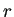 が一意的に存在するが、
Mod[
が一意的に存在するが、
Mod[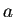 ,
, 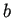 ,
, 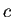 ] はこの
] はこの 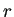 を表す。
を表す。
ゆえに
r=Mod[x,2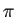 ,-
,-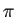 ] とすると、
(
] とすると、
(
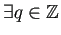 )
)
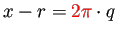 ,
,
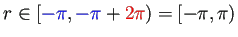 .
. 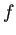 が周期
が周期 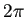 であるから
であるから 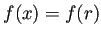 .
.