6.4 Python による Jordan 領域の等角写像の計算プログラム

$\Omega=D_1$ の等角写像を考えよう。$\Omega$ と $D_1$ が等しいので、 $\Omega$ から $D_1$ への双正則写像として、 恒等写像 $\mathrm{id}(z)=z$ が取れるのは自明である。

正規化条件によっては、それ以外のものが得られる。実際、 $z_0\in\Omega$ として、$\Omega$ の写像関数 $\varphi\colon\Omega\to D_1$ のうち、正規化条件

$$\varphi(z_0)=0,\quad \varphi'(z_0)>0$$

を満たすものは、実は1次分数変換

$$\varphi(z)=\frac{z-z_0}{1-\overline{z_0}z}$$ (6.5)

であることが知られている。$z_0=0$ のとき、 $\varphi=\mathrm{id}$ となる訳である。

ここでは、前項で説明した天野の方法で $\Omega$ の近似等角写像を求めて、 真の等角写像 (2.7) と比べてみることにする。

(答えの分かっている問題を解くことによって、 アルゴリズムやプログラムの正しさをチェックする、 というしばしば使われるテクニック。)

天野の方法では、 $\left\{\zeta_k\right\}_{k=1}^N$, $\left\{z_j\right\}_{j=1}^N$ を適切に選ぶ必要があるが、 今の場合は $\Omega$ は円盤領域であるから、 $\left\{\zeta_k\right\}_{k=1}^N$として

$$\zeta_k=R \exp\frac{2\pi i k}{N}$$   ( $k=1,\cdots,N$)   ($R$ は $1$ より大きい数)$$,$$

$\left\{z_j\right\}_{j=1}^N$ として

$$z_j= \exp\frac{2\pi i j}{N}$$   ( $j=1,\cdots,N$)$$.$$

を採用するのが自然であろう。$R$ として、とりあえず $R=2$ で計算してみる。

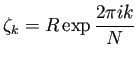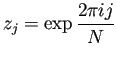conformalmap.py

/Users/mk/.tex-inputs/potential-progs/conformalmap.py

conformalmap-v2.py

/Users/mk/.tex-inputs/potential-progs/conformalmap-v2.py

図: 天野の方法による近似等角写像