普通の熱方程式 (![[*]](crossref.png) ) の代わりに
) の代わりに
|
(3) |
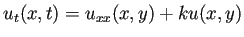 ( (
 ) ) |
を考えてみよう。ここで 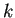 は任意に与えられた実数とする。
は任意に与えられた実数とする。
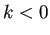 の場合は、棒をとりまく空気の温度が
の場合は、棒をとりまく空気の温度が 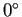 で、
棒が熱的に絶縁がされていなくて、Newtonの冷却の法則に従って、
空気中に熱が逃げる、というように解釈できる。
で、
棒が熱的に絶縁がされていなくて、Newtonの冷却の法則に従って、
空気中に熱が逃げる、というように解釈できる。
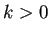 の場合は、(やや人工的な想定かもしれないが)
棒の各部分で温度に比例した熱が発生する状況と考えられる。
の場合は、(やや人工的な想定かもしれないが)
棒の各部分で温度に比例した熱が発生する状況と考えられる。
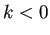 の方がリアリスティックかもしれないが、
ここでは
の方がリアリスティックかもしれないが、
ここでは 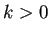 の場合を考えてみよう。
境界条件としては、まずは
の場合を考えてみよう。
境界条件としては、まずは
|
(4) |
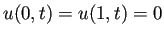 ( (
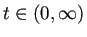 ) ) |
を考えてみよう。
プログラム作成はかなり簡単な方で、差分方程式を
プリント [4] の (43) から
|
(5) |
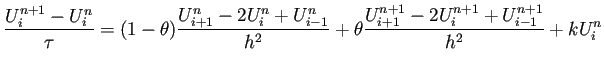 |
に置き換えればよい。あるいは (46) の右辺に
を加えるだけ、という方が親切か。
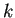 を色々変えて試してみること。実は
を色々変えて試してみること。実は
ある 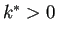 が存在して、 が存在して、
が成り立つ。
|
境い目である 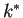 の値はどれくらいだろうか
(二分法で求められる)。
差分法の分割を十分細かくしてやってみよう
(差分解では境目の値は
の値はどれくらいだろうか
(二分法で求められる)。
差分法の分割を十分細かくしてやってみよう
(差分解では境目の値は 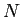 の値によるので、
ある程度大きな
の値によるので、
ある程度大きな 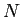 を固定したら、それを変更せずに二分法をすること)。
これはしばらくクイズとしたい。
初期値境界値問題の解はっきり書くことが出来るので証明は難しくないが、
結果はかなり意外かもしれない (この辺は人によるだろうけれど、
私は初めて知ったときはびっくりしました)。
それが出来たら説明して下さい。
を固定したら、それを変更せずに二分法をすること)。
これはしばらくクイズとしたい。
初期値境界値問題の解はっきり書くことが出来るので証明は難しくないが、
結果はかなり意外かもしれない (この辺は人によるだろうけれど、
私は初めて知ったときはびっくりしました)。
それが出来たら説明して下さい。
桂田 祐史
![]() の場合は、棒をとりまく空気の温度が
の場合は、棒をとりまく空気の温度が ![]() で、
棒が熱的に絶縁がされていなくて、Newtonの冷却の法則に従って、
空気中に熱が逃げる、というように解釈できる。
で、
棒が熱的に絶縁がされていなくて、Newtonの冷却の法則に従って、
空気中に熱が逃げる、というように解釈できる。
![]() の場合は、(やや人工的な想定かもしれないが)
棒の各部分で温度に比例した熱が発生する状況と考えられる。
の場合は、(やや人工的な想定かもしれないが)
棒の各部分で温度に比例した熱が発生する状況と考えられる。
![]() の方がリアリスティックかもしれないが、
ここでは
の方がリアリスティックかもしれないが、
ここでは ![]() の場合を考えてみよう。
境界条件としては、まずは
の場合を考えてみよう。
境界条件としては、まずは
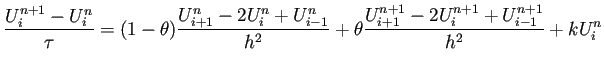
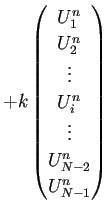
![]() を色々変えて試してみること。実は
を色々変えて試してみること。実は