2 次週から

heat1d-i-glsc.c, heat1n-i-glsc.c をたたき台にしたプログラムを使って数値実験する。

「発展系の数値解析」の輪講.

1. 1 (短いお話), 2 差分近似
   7 補足 (1) ランダウの記号 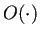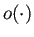$O(\cdot)$, $o(\cdot)$ について、を見ておくこと。
2. 3 熱方程式の陽的差分法による解法
3. プログラム heat1d-e-glsc.c の説明
4. 4 (1) 解析解との比較
   表の1 と図2の再現. 補足 7(2) 対数グラフの読み方、を見ておくこと。
5. 4 (2) 解の漸近挙動
   図 3〜図8, 図9〜図14, 表2 の再現
6. 4 (3) 熱伝導方程式の平滑化作用, 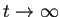$t\to\infty$ の際の漸近形
   図15〜図20の再現 (Fourier 級数の議論少し分かりにくいかも。)
7. 5 陰解法 (1)と(2)
   図29〜32の再現
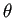8. 5 (3) $\theta$法, クランク-ニコルソン法
   heat1d-i-glsc.c の説明
9. 7(3) 熱伝導方程式の解の指数関数的減衰
10. 7(4) 連立1次方程式((46)が解けること
11. 7(5) 差分解の厳密解への収束 (定理2) の証明
    これは希望する人にやってもらう？
12. 7(6)ガウスの消去法のアリゴリズム
    もし出来れば、 heat1d-i-glsc.c の中にある trilu(), trisol() の解説をする。