Next: 参考文献
桂田 祐史
Date: 2020年4月16日
自分で適当に探してもらえると嬉しいが、 手頃そうなものをあげておく (私がそれなりに知っているので、アドバイスしやすい)。
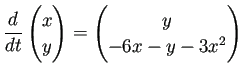
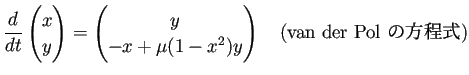
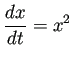 (
(
桂田 [4] を見よ (これは藤田・齊藤 [8] の読書ノートのようなもので、 [8] を持っているのならば、そちらを読んだ方が良いかも。 あるいは、 富坂・花輪・牧野 [10] のような天文学の本を読むとか。)。
一般化して、三体問題、多体問題に取り組むのも面白いかも。 三体問題には、有名な特解が色々ある (SF にも時々出て来る)。 そういうのをシミュレーションするのに誰かチャレンジしないかな、 と考えている。 最近出た浅田 [11] なども面白く読めるかも。
| (2) | 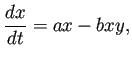 | |
| (3) | 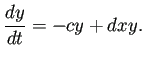 |
簡単なところは、 桂田研の卒業研究レポート長谷川 [8] で読める。 [8] には、 三つの種を考えた一般化である May-Leonard のモデルも出て来る。
| (4) | ![$\displaystyle \left\{ \begin{array}{ll} \dfrac{\D x}{\D t}=-\sigma x(t)+\sigma ...
...t)-y(t)-x(t)z(t) [1em] \dfrac{\D z}{\D t}=-bz(t)+x(t)y(t) \end{array} \right.$](img36.png) |
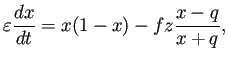 | ||
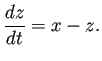 |