5.1 p98 (プログラムリスト1)

98ページのプログラムで、97-100ページの計算実習1をやってみる。

% ./p98
 INPUT : N=
4
 INPUT: EPS=
1E-5
 INPUT : M =
100
 INPUT : A(  1,  1)=
5
 INPUT : A(  1,  2)=
4
 INPUT : A(  1,  3)=
1
 INPUT : A(  1,  4)=
1
(中略)
 INPUT : A(  4,  1)=
1
 INPUT : A(  4,  2)=
1
 INPUT : A(  4,  3)=
2
 INPUT : A(  4,  4)=
4
 INPUT:X(  1)=
1
 INPUT:X(  2)=
1
 INPUT:X(  3)=
1
 INPUT:X(  4)=
1
 (NITER,EVAL,ERROR)=           1   8.46153831       1.00000000
 (NITER,EVAL,ERROR)=           2   6.80000019      0.244343832
 (NITER,EVAL,ERROR)=           3   5.61643887      0.210731626
(中略)
 (NITER,EVAL,ERROR)=          16   1.00001359       3.26867419E-04
 (NITER,EVAL,ERROR)=          17   1.00000048       1.31130155E-05
 (NITER,EVAL,ERROR)=          18  0.999999940       5.36441860E-07
0NO．OF ITERATIONS =  18   EPS=  1.0000E-05
0EIGENVALUE=  1.0000E+00
0**EIGENVECTOR**
   I     X(I)      I     X(I)      I     X(I)      I     X(I)      I     X(I)
   1  7.0708E-01   2 -7.0713E-01   3  5.4529E-05   4  3.8838E-05
%

これが97ページの記述と合っているか。微妙に食い違っている？？

$$A= \begin{pmatrix} 5 & 4 & 1 & 1\\ 4 & 5 & 1 & 1\\ 1 & 1 & 4 & 2 \\ 1 & 1 & 2 & 4 \end{pmatrix}$$

$$\bm{x}_0=\begin{pmatrix}1 \\ 0 \\ 0 \\ 0 \end{pmatrix}$$

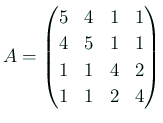
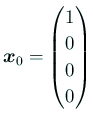
から始めると、すぐに 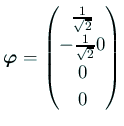$\bm{\varphi}= \begin{pmatrix}\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} 0 \\ 0 \\ 0 \end{pmatrix}$ に近く。

$$\bm{x}_0=\begin{pmatrix}1 \\ 1 \\ 1 \\ 1 \end{pmatrix}$$

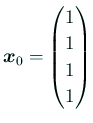
から始めると、本当は $(\varphi,\bm{x}_0)=0$ なので、 $\varphi$ に収束するはずはないが、「実際には 上記のように反復回数は大きいが正しい値に収束した.」 とテキストに書いてあるが、 C で書いたプログラムではそうはならなかった。 これは単精度と倍精度の違いであろう。 試しに double を float にしたら、 FORTRAN プログラムと同じ結果を出力した。