Next: 参考文献 Up: コンピューター実習 Previous: A. 現象数理学科 Mac に
各自やってみよう。 全員に [8] くらいまでやってもらいたい。
何かを参考にしても、人に尋ねても良い。自分自身が納得して、 似たような問題が解けるようになることが大事。
ときどき「どこまで出来ました?」尋ねます。
最後の [11], [12] はそのうち時間を取ってやるかも。
いつでも気軽に (メールでも可) 質問・相談してください。
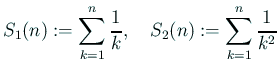
を計算するプログラムを書け。 計算結果は double の精度一杯まで表示せよ。
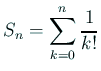 を計算して結果を表示するプログラムを
書け (
を計算して結果を表示するプログラムを
書け (
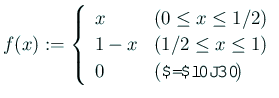
の場合に
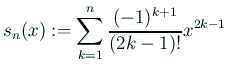
を計算する関数を書き、
x = r * sin(theta) * cos(phi); y = r * sin(theta) * sin(phi); z = r * cos(theta); |
d2p(x, y, z, &r, &theta, &phi); |
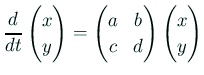 ,
,
(
![]() は狭義単調減少で、
は狭義単調減少で、
![]() ,
,
![]() であるから、
区間
であるから、
区間 ![]() にただ1つの実数解を持つことが分かる。)
にただ1つの実数解を持つことが分かる。)
桂田 祐史