秋休みの宿題
桂田 祐史
Date: 2017年10月27日
次回ゼミは11/17です。
休み中に、問(ii) までやっておくこと。
プログラム動かなければ質問に来て下さい。
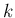 を実数の定数として
を実数の定数として
という初期値境界値問題を考える。
- (i)
- heat1d-i-glsc.c は、
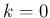 に対して問題を解くプログラムである。
ユーザーが入力した
に対して問題を解くプログラムである。
ユーザーが入力した 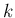 に対して問題を解くようにプログラムを
書き直しなさい (プログラムの名前は適当に変えること)。
に対して問題を解くようにプログラムを
書き直しなさい (プログラムの名前は適当に変えること)。
- (ii)
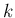 が小さいうちは、任意の
が小さいうちは、任意の 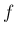 に対して
に対して
が成り立つが、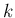 がある値
がある値 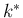 を超えると、これが成り立たなくなる。
この
を超えると、これが成り立たなくなる。
この 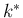 の値を実験的に求めよ。
いくつか注意
の値を実験的に求めよ。
いくつか注意
- (a)
- (実は、差分方程式の解の場合、
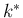 は
は 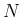 に依存する、
つまり
に依存する、
つまり 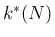 と書くべき)
実験をしている間は、
と書くべき)
実験をしている間は、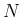 の値は一定にしておくこと。
の値は一定にしておくこと。
- (b)
-
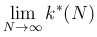 が微分方程式の場合の
が微分方程式の場合の 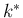 に収束する。そういう意味で、
に収束する。そういう意味で、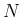 はある程度大きいもので計算すること。
出来れば、複数の
はある程度大きいもので計算すること。
出来れば、複数の 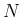 に対して
に対して 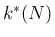 を求めておくこと。
を求めておくこと。
- (iii)
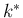 は何だろう?当てずっぽうでも良いから予想してみよう。
(真面目にやると、(1),(2),(3) の厳密解を求めることになる。)
は何だろう?当てずっぽうでも良いから予想してみよう。
(真面目にやると、(1),(2),(3) の厳密解を求めることになる。)
- (iv)
- ちなみに (2)の代わりに
|
(4) |
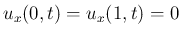 |
とした場合は、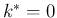 である。
それは heat1n-i-glsc.c を書き換えて実験出来る。
確かめよ。
である。
それは heat1n-i-glsc.c を書き換えて実験出来る。
確かめよ。
- (v)
- さらに (2)の代わりに
|
(5) |
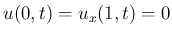 |
とした場合は、また違う 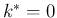 の値になる。その値はいくつか。
(これもプログラムを書き換えて実験出来るけれど、
書き換えが少し難しいかもしれない。)
の値になる。その値はいくつか。
(これもプログラムを書き換えて実験出来るけれど、
書き換えが少し難しいかもしれない。)
境界条件を変えたとき、プログラムをどのように書き換えるかは、
「熱方程式に対する差分法I」の第1章
http://nalab.mind.meiji.ac.jp/~mk/labo/text/heat-fdm-1.pdf
を見て下さい。
桂田 祐史
2017-10-27
![]() を実数の定数として
を実数の定数として